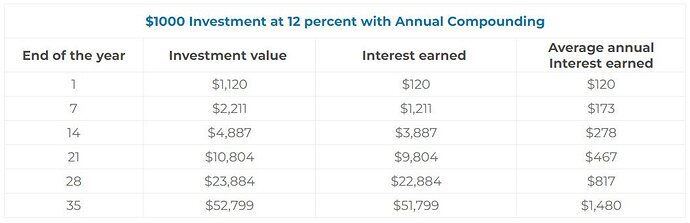How the time value of money applies to Real Estate Valuation - (It’s Rocket Science)
When it comes to real estate, there are a lot of factors that go into the valuation process. Understanding the time value of money is among one of them. This principle states that money available at present is worth more than the same sum in the future due to its earning potential.
Often, students and analysts learn about more complicated ways to value things like the internal rate of return (IRR) and net present value (NPV) in a way that doesn’t make sense to them. The time value of money (TVM) is the fundamental concept that underlies the IRR and NPV approaches.
This article will walk you through the important concept of the time value of money, and then you will find some examples of why it’s so crucial to understand the impact of the timing of cash flows on a real estate investment.
Key Takeaways
- Time value of money means that a dollar today is worth more than a dollar tomorrow.
- The time value of money is also compounded, which means that the value of money invested today will grow over time.
- When valuing a property, the time value of money and compound interest are important concepts to understand.
- By discounting future cash flows and applying compound interest, we can get a more accurate estimate of a property’s value.
What is the time value of money in real estate?
Time value of money definition:
It is the idea that one dollar today is worth more than one dollar tomorrow. The dollar today can be invested and earn interest, while the dollar tomorrow cannot.
This principle depends on compound interest, which states that earnings on an investment will grow at a compounded rate over time.
The earnings from the initial investments will be reinvested and then earn interest on top of that. So, the value of money grows over time as long as it is invested in a compounding interest account.
Let’s understand the concept of the time value of money with an example -
Assume a $250 investor is weighing three 10-year investment options. These are the alternatives:
- Plan A: The investor gets $20 after the first year and the original $250 after ten years.
- Plan B: The investor gets $2 every year for ten years, plus the original $250.
- Plan C: After the tenth year, the investor will receive $20 plus the original $250.
Each plan pays out $250 plus $20 every year for ten years.
Which strategy should the investor choose?
Plan A is the best option for the investor. Why? Because when money is received, it can be allocated to one of two purposes.
The investor could use the funds to treat a friend to dinner. Second, the money can be invested by the investor.
By spending or reinvesting the $10 acquired at the end of year 1, the investor has the greatest possibility to spend the money or earn interest throughout the 10-year term with Plan A.
Plan A allows him to invest ten dollars for nine years and earn more interest than Plan B allows for ten one-year investments of $1 each. Because of the possibility to collect interest, investors who plan to reinvest their returns prefer earlier returns over later ones.
Early returns are preferred by real estate investors who consume their gains simultaneously. Would you want to wait ten years to take your friend out to dinner, as Plan C requires?
Learn More
Timeline in time value of money
Panel A of the below figure depicts a timeline, which serves as visual assistance for visualising the time pattern of money returns.
Beginning on the left with the present, time 0, and ending on the right with the terminal time point, N, the line is broken into time points and time intervals, or periods.
When reviewing single-property investments, annual periods are commonly utilised. However, monthly periods are sometimes suitable (for example, when analysing mortgage or lease payments).
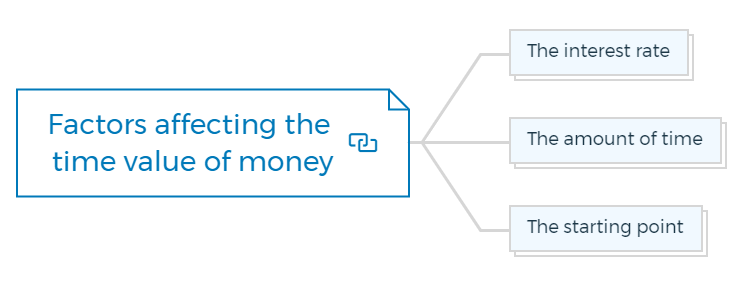
Factors affecting the time value of money
A few factors will affect the time value of money in a real estate context. These include:
The interest rate
The higher the interest rate, the greater the impact of compound interest on the value of money.
The amount of time
The longer the period, the greater the impact of compound interest.
The starting point
The earlier the cash flow begins, the greater the impact of compound interest.
You are missing out if you haven’t yet subscribed to our YouTube channel.
Importance of time value of money in real estate
The time value of money is one of the most important concepts in real estate investment.
- It considers that cash flows from a real estate investment are not always received simultaneously.
When valuing a property, it’s important to discount future cash flows back to their present value. You can do this by using an appropriate discount rate, the interest rate you would need to earn to have the same buying power as the cash flow in question.
This discount rate is based on the time value of money and considers both the amount of time and the uncertainty of whether or not it will occur.
When you’re trying to decide whether or not to invest in a property, it’s important to look at the investment’s net present value (NPV).
The NPV is calculated by summing up all the cash flows associated with the investment and then discounting them to their present value.
It considers both the positive and negative cash flows and measures whether or not the investment is worth making.
- The time value of money is also important for refinancing a property.
You exchange one set of future cash flows for another when you refinance. It’s important to ensure that the new cash flows are worth more than the old ones; otherwise, you’re not gaining anything by refinancing.
- Finally, the time value of money is important for selling a property.
When you sell a commercial property, you exchange all future cash flows for a lump sum of cash from the investment. It’s important to ensure that the lump sum is worth more than the future cash flows; otherwise, you’re not gaining anything by selling.
In short, the time value of money is a very important concept in real estate investment. You can better understand the basic financial concept of real estate deals and make more informed investment decisions by understanding them.
CAUTION
Present Value:
The present value of a cash flow is the amount of money required today to invest in an asset that would generate the same cash flow stream in the future.
Discount Rate:
The discount rate is used to determine the present value of cash flows received in the future.
Future Value:
The future value is the amount of money that will be received due to an investment made today.
Periodic Rate:
The periodic rate is the interest rate compounded at regular intervals.
Number of Periods:
The number of periods is the number of times the interest rate is applied to the principal amount.
Lump-sum:
In a certain period, one-time expenditure.
Equations for calculating the time value of money
Compounding in real estate
The first two time-value-of-money (TVM) procedures are utilized to determine future values resulting from compounding interest. Compound interest is when an investor earns interest on the principal and the accrued interest.
Calculate the future value of a lump sum
Assume $1,000 is invested in an investment account managed by a financial advisor today.
The investor plans to take the original investment plus accrued earnings at the end of 6 years, and the account is predicted to produce a 7.5 % annual compounded return.
Panel A shows the cash inflows and outflows in a timeline format for this situation.
The present value (PV) of $1,000 invested at time zero is transformed to a future value (FV) at the end of 6 years to solve this problem.
The PV is multiplied by the future value interest factor (FVF) for the selected interest rate and the time to make the conversion. The calculation for converting a present value into a future value is -
Future value of lump sum formula
IMPORTANT
FV = PV X FVF (7.5 percent, six years)
= $1000 X 1.54
= $1,543.30
The solution to the future value of a lump sum equation is the FVF of 1.54, assuming that $1 is invested at 7.5% for 6 years.
It shows that $1 invested now at 7.5% for six years will grow (compound) to $1.54 at the end of 6 years (assuming annual compounding). As a result, if you invest $1,000 today, it will rise to $1543.30 in six years.
To solve this problem, you’ll need to use the following keystrokes on your calculator:
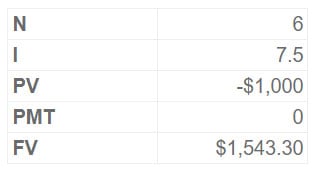
The $1,000 lump sum investment is entered as a negative figure, indicating an outflow (i.e., cash paid) from the investor’s perspective.
Entering N, I, PV, and PMT (the “knowns”) into a calculator and pressing the FV key (the “unknown”) yields the $1543.30 solution.
With a 12 percent interest rate, $1,000 invested now will increase to $1,973.82 in six years. The calculator keystrokes and conversion equation are listed below.
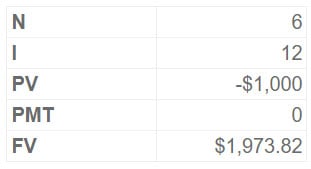
IMPORTANT
FV = PV X FVF (12%, six years)
= $1,000 x 1.97
= $1,973.82
It’s worth noting that you can figure out the fifth if you know four of the five essential inputs.
Consider the case where the future value of $1,973.82 is known, but I, the yearly interest rate, is unknown. You can obtain a solution of 12% by entering $1,973.82 in the FV register (along with N = 6, PV = -$1,000, and PMT = 0) and pressing the I key.
Quick Tip
Try it Now
You’ve arranged to buy a piece of property for $300,000 today. You plan to keep the house for ten years before selling it. You estimate the property’s value to rise at 17% annually, compounded annually. In ten years, how much should you be able to sell the home for?
Remember - TVM computations are frequently rounded to the nearest hundred-dollar figure or even to the nearest thousand dollar amount by industry professionals.
Why? Because while TVM computations are mathematically exact, the results are dependent on a set of assumptions that may or may not be correct. In many circumstances, displaying data with digits to the right of the decimal point may provide the impression of precision that does not present.
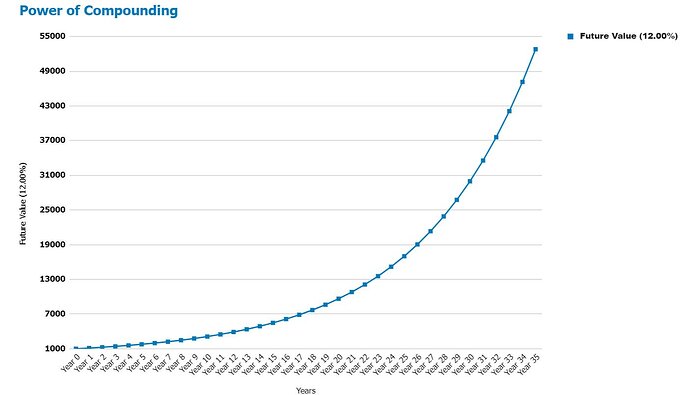
The Effect of Compounding
We explore the growth rate in the $1,000 investment above in greater detail to demonstrate the power of compounding.
The below table depicts how much the lump sum investment will grow, assuming interest is compounded (paid) annually and the investor does not remove any of the $1,000 initial investment or interest earnings.
The value of the investment remains constant throughout the year because of annual compounding. The accumulated investment amount rises by the interest generated during the first year at the end of the year.
If the investor withdraws the money after a year, the total value of the investment will be $1,120, which includes the $1,000 initial investment plus $120 in interest income.
After seven years, the aggregate investment value will be $2,211, equal to the $1,000 investment plus $1,211 in interest income. By the completion of the 35th year, the investment will be worth $52,799.
It’s worth noting that the average amount of interest earned goes up as the length of time goes on. It is because interest is being earned on a larger and larger investment.
As a result, the longer an investment is allowed to compound, the more powerful compounding becomes!
The below graph shows the growth of a $1,000 investment over time using annual compounding at 12%. It’s worth noting that the slope of the curve rises as the investment holding term lengthens.
Interest is compounded annually in this example. On the other hand, banks and other borrowers frequently pay interest monthly or even daily.
Learn More
The table below compares the accumulated investment values for a $1,000 investment assuming monthly and daily compounding to the accumulated investment values assuming annual compounding.
With monthly compounding, a $1,000 investment will grow to $2,307 over seven years, compared to $2,211 with yearly compounding. The investment will have grown to $2,316 in seven years due to the daily compounding of interest.
As the investing time horizon grows longer, the impacts of more frequent compounding become more obvious. We’ll presume that compounding frequency is the same as the frequency with which the payments are made or received unless otherwise indicated.
If cash flows are received yearly, we shall assume annual compounding.
Quick Tip
Try it Now
Assume a $1,000 investment is made for 15 years. Although the annual interest rate is 12%, the interest is compounded quarterly. What is the value of N? What is the interest rate quarterly? In ten years, what will the total FV be?
How To Finance Your Property Development Project?
And Other Books On Real Estate Development Finance
Includes 5 x detailed eBooks
✓ Property Development Finance: Easily Finance Your Project? (26 Pages)
✓ 10 Big (Financial) Property Investing Mistakes Made By Investors (58 Pages)
✓ 10 Finance Options For Your Next Property Development Project (29 Pages)
✓ What Is Equity Finance And How Does It Work? (42 Pages)
✓ Property Investment Finance - Ultimate Guide
Calculate the future value of the annuity
Assume the investor intends to invest $1,000 in a 7.5% yearly compounded investment at the end of each year and wants to know how much these six investments will be worth.
Solving this problem entails determining the future value of an annuity, as indicated in panel B of the figure of timeline demonstration for compounding problems.
The $1,000 annuity (i.e., cash investments at the end of each period) is converted into future values using future value factors for annuities (FVFA).
Future value of annuity formula
FVA = Annuity X FVFA (7.5%, six years)
= $1000 X 7.24
= $7,244.02
The FVFA of 7.24402 is the answer to the future value of an annuity equation at 7.5% for six years. It shows that investing $1 at the end of each year for six years at 7.5% yields $7.24402 at the end of the six years.
As a result, a $1,000 investment over six years will rise to $7,244.02. The keystrokes on the calculator are
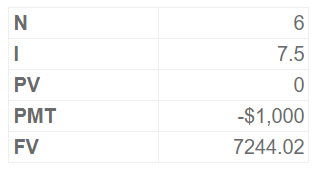
The future value is, once again, unknown. The level payment is entered as a negative number in the PMT register. The PV register includes a zero amount (or is empty) for calculating the future value of a series of level payments (investments).
This instructs the calculator to invest the money every year for N years. Remember that the one-time investment is entered in the PV register when calculating the future value of a lump sum—the PMT register contains a zero or is empty.
Finally, suppose the investor wants to make monthly investments of $83.33 ($1,000 12) over the next six years. The monthly interest rate, I, is 0.625 per cent (7.5 percent/12) in this case, and N is 72 (6X12).
FVA = Annuity X FVFA (7.5%/12, 72 months)
= $83.33 X $90.58
= $7,547.93
The relevant keystrokes are
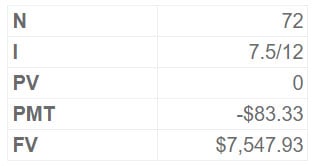
Regardless of whether payments are made monthly or annually, the investor will invest $1,000 every year in this example.
If monthly payments of $83.33 are made, however, after six years, the investor will have $7,547.93, compared to $7,244.02 with annual investments.
Why is there a $303.9 difference in future values when both methods have the same total payments throughout the six years? In the monthly compounding scenario, the initial investment occurs at the end of month 1, whereas in the yearly compounding scenario, it occurs at the end of year 1.
As a result, monthly investments begin to earn interest 11 months earlier than annual installments.
Quick Tip
Try it Now
You pay $100,000 for a piece of land today. How much must you sell the property in 20 years to obtain a 12% yearly return on your initial $100,000 investment and the $1,500 monthly tax and insurance payment? Assume these funds might provide a 12% annual return with equivalent risk.
Calculate the future value of an annuity due
What if the investor wants to invest $1,000 every year for the next six years? These situations are the " future value of an annuity due." problems.
The total interest received over the five years will increase since the initial and subsequent $1,000 annual payments are brought forward a year.
Users of financial calculators can easily specify that cash flows should be invested or received at the start of each period (“begin mode”) rather than at the end (“end mode”). Other than that, the keystrokes are the same.
The future value of this annuity due is $7,787.32, which is $543.3 more than the $7,244.02 accumulated value assuming year-end deposits. What is the link between the annuity due result and the predicted future value result?
Note that you can get the $7,787.32 annuity due solution by multiplying the standard annuity problem solution by 1 plus the monthly interest rate [i.e. $7,787.32 = $7244.02 (1 + 0.075)].
Assume that a 12-unit apartment building owner will put $1,200 in an interest-bearing reserve account each year, or $100 per unit. After seven years, the proceeds will be utilised to recondition the units.
What will the total value of the reserve account be at the end of seven years if the deposits are made at the beginning of each year and earn 7.5% interest compounded annually?
Continued at…
Using time value of money for real estate valuation [Part 2-2]